Introduction

The 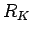correlation coefficient is a generalization of Pearson's correlation coefficient, see for example http://mathworld.wolfram.com/CorrelationCoefficient.html and have similar properties in respect to least squares as in the Pearson case, see eg. http://mathworld.wolfram.com/LeastSquaresFitting.html.

Here the 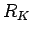correlation coefficient extends to K-dimensional data points and an expected covariance can be defined:

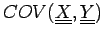
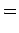
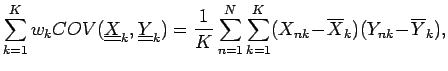
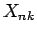
where and elements of the NxK table 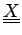. with columns 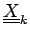. The correlation coefficient is

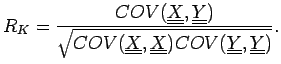
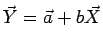
For a linear fit it can be shown that it has similar properties as in the Pearson case, where

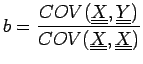
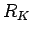
can be discretized to obtain an equivalent for Matthews correlation coefficient:

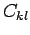
where are the elements of the confusion matrix.

For more details see the reference below:

Reference
Comparing two K-category assignments by a K-category correlation coefficient
J. Gorodkin, Computational Biology and Chemistry, 28:367-374, 2004.

Abstract of the reference:
Predicted assignments of biological sequences are often evaluated by Matthews correlation coefficient. However, Matthews correlation coefficient applies only to cases where the assignments belong to two categories, and cases with more than two categories are often artificially forced into two categories by considering what belongs and what does not belong to one of the categories, leading to the loss of information. Here, an extended correlation coefficient that applies to K-categories is proposed, and this measure is shown to be highly applicable for evaluating prediction of RNA secondary structure in cases where some predicted pairs go into the category ``unknown'' due to lack of reliability in predicted pairs or unpaired residues. Hence, predicting base pairs of RNA secondary structure can be a three category problem. The measure is further shown to be well in agreement with existing performance measures used for ranking protein secondary structure predictions.